司 法 鉴 定 技 术 规 范

SF/Z JD0105010——2018

______________________________________________________________________________________________

常 染 色 体 STR 基 因 座 的 法 医 学 参 数 计 算 规 范

Specification of the calculation methodology of forensic parameters for autosomal STR

2018-11-08 发布 2019-01-01 实施

中华人民共和国司法部公共法律服务管理局 发 布

目 次

前言

引言

1. 范围

2. 术语和定义

3. 群体遗传学参数计算

参考文献

前 言

本技术规范按照GB/T 1.1-2009给出的规则起草。

本技术规范由司法鉴定科学研究院提出。

本技术规范由司法部公共法律服务管理局归口。

本技术规范起草单位：司法鉴定科学研究院、四川大学华西基础医学与法医学院。

本技术规范主要起草人：李成涛、张素华、侯一平、边英男、刘希玲、李莉。

本技术规范为首次发布.

引 言

本技术规范运用法医物证学、遗传学和统计学等学科的理论，结合法医物证鉴定的实践需求而制订， 为法庭科学采用常染色体STR基因座进行法医物证鉴定所涉及的法医学参数计算提供科学依据和统一标准。

常 染 色 体 STR 基 因 座 的 法 医 学 参 数 计 算 规 范

1. 范围

本技术规范规定了采用常染色体STR基因座进行法医物证鉴定的群体遗传学参数计算。

2. 术语和定义

下列术语和定义适用于本文件。

2.1 基因座 locus

基因在染色体的特定位置。

2.2 等位基因 allele

基因座上的基因可以有多种形式，它们之间存在DNA一级结构的差异，这种有差异的基因互称为等位基因。

2.3 基因型 genotype

个体在一个或者多个基因座上等位基因的组合，生物体可见性状的实际基因组成。

注：对一个基因座而言，指基因座上成对等位基因的组成。

2.4 杂合子 heterozygote

对一个基因座而言，成对等位基因不同时，基因型表现称为杂合子。

2.5 纯合子 homozygote

对一个基因座而言，成对等位基因相同时，基因型表现称为纯合子。

2.6 遗传多态性 genetic polymorphism

控制遗传标记的基因座上存在两个或两个以上等位基因，且最小等位基因频率大于0.01；同时等位基因在群体中能够保持稳定的频率，可认为该基因座具有遗传多态性。

2.7 Hardy-Weinberg 平衡定律 Hardy-Weinberg equilibrium

用于阐述繁殖对群体的基因频率和基因型频率的影响。该定律建立在一个理想的群体模式上，即群体无限大、随机婚配、没有突变及没有大规模的迁徙和没有选择因素的影响，结论是群体中的基因频率和基因型频率在逐代传递中保持不变。

2.8 乘积定律 product rule

用于计算多个独立遗传标记的基因型组合的方法。

注：应用乘积定律的先决条件是所检测的各个遗传标记之间具有独立性。

2.9 连锁不平衡 linkage disequilibrium, LD

群体水平上不同标记之间等位基因的非随机性关联。

注：在遗传过程中，处于连锁不平衡状态基因座上的等位基因具有共同遗传的趋势，群体中的单倍型频率会高于或者低于应用乘积定律计算出的频率。

2.10 连锁平衡 linkage equilibrium, LE

位于不同染色体上的基因座，或者位于同一条染色体但相距较远的基因座常按照随机组合原则进行遗传，呈不连锁遗传状态，这种基因座之间没有相关性的状态称之为连锁平衡。

注：各个遗传标记处于连锁平衡状态，表明各遗传标记相对独立，可采用乘积定律分析它们的累积概率。

3. 群体遗传学参数计算

3.1 Hardy-Weinberg 平衡定律检验

检验方法有吻合度检验法、纯合度检验法、似然比检验法及确切概率分析法等。其中，吻合度检验法最为常用。对处于Hardy-Weinberg平衡状态的调查群体，可认为纯合子基因型频率等于该基因座上等位基因频率的平方，杂合子基因型频率等于该基因座上两个等位基因频率乘积的两倍。可采用Arlequin、PowerMarker、GenAlex、PowerStats及STRAF等软件进行Hardy-Weinberg平衡检验。

注：由于在实际中“理想群体”是不存在的，在应用群体调查资料计算法医学参数之前，需首先检验对象群体是否是统计学意义上的Hardy-Weinberg平衡群体。

3.2 基因座独立性分析

常采用2╳2统计表或者卡方检验，也可采用Arlequin、PowerMarker、PLINK等软件。

注：对一组遗传标记进行独立性分析是判断遗传标记能否应用乘积定律的前提。

3.3 频率计算

频率计算可采用直接计数法，也可采用PowerMarker、GenAlex、PowerStats及STRAF等软件。

3.3.1 基因型频率

指处于Hardy-Weinberg平衡状态的调查群体中，单个基因座上的某种基因型在全部基因型中所占的百分比。计算公式如下：

注：单个基因座上全部基因型频率的总和应为1。

3.3.2 等位基因频率

指处于Hardy-Weinberg平衡状态的调查群体中，某种等位基因数目占该基因座上所有等位基因数目的百分比。计算公式如下：

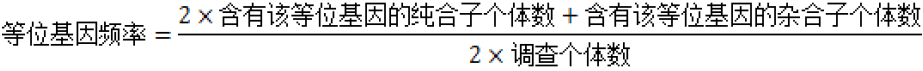
注：单个基因座上全部等位基因频率的总和应为1。

3.4 法医学参数

可采用PowerMarker、GenAlex、PowerStats及STRAF等软件进行计算。

3.4.1 杂合度 heterozygosity, H

指调查群体中某遗传标记所有基因型中杂合子的占比。杂合度越高，说明该遗传标记的杂合性越大， 在法医学个人识别中的应用价值越大。杂合度分为观察杂合度（observed heterozygosity, Hobs）和期望杂合度（expected heterozygosity, Hexp）。计算公式分别如下：

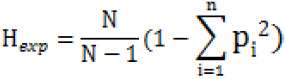
式中：N为调查群体中所有等位基因或单倍型的总数，n为等位基因或单倍型种类的数目，P_i为第i个等位基因或单倍型的频率。

3.4.2 个体识别能力 discrimination power, DP

在调查群体中随机抽取两个体，二者的遗传标记基因型不相同的概率，是评价遗传标记系统识别不同个体效能大小的指标。常见计算公式如下：

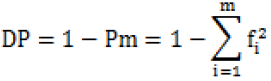
式中：m为某一遗传标记的表型数目，f_i为第i个表型的频率，

指调查群体中随机抽取两个无关个体在某一个基因座上二者表型纯粹由于机会而一致的概率。

另外，个体识别能力也可以基于等位基因频率进行计算。计算公式如下：

式中：n为等位基因的数目，P_i为基因座上第i个等位基因的频率。

上述公式是对于单个遗传标记而言的。个体识别不止使用一个遗传标记，一组相互独立的遗传标记识别群体中不同个体的综合能力，即累积个体识别能力（total discrimination power, TDP）。计算公式如下：

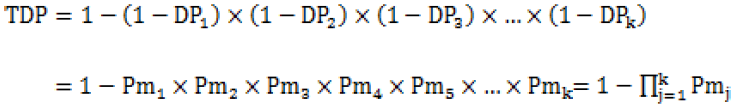
式中：k为遗传标记的数目， 为检测系统中第j个遗传标记的Pm值，

为检测系统中k个遗传标记的总Pm值。

3.4.3 非父排除概率 probabilityof exclusion, PE

不是孩子生父的男子能够被某个遗传标记系统排除的概率，用于评估某一遗传标记系统在亲权鉴定案件中的实际价值。遗传标记系统的多态性程度越高，可用于排除非生物学父亲的能力越强。

1）常染色体STR基因座应用于三联体亲权鉴定的非父排除概率计算公式：

式中：n为等位基因的数目，p_i为基因座上第i个等位基因的频率，p_j为基因座上第j个等位基因的频率。

2）常染色体STR基因座应用于二联体亲子鉴定的非父排除概率计算公式：

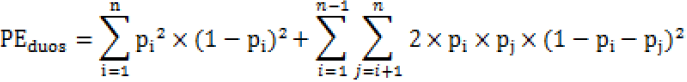
式中：n为等位基因的数目，p_i为基因座上第i个等位基因的频率，p_j为基因座上第j个等位基因的频率。

上述公式是对于一个遗传标记而言的。亲权鉴定不止使用一个遗传标记，一组相互独立的遗传标记可采用累积非父排除概率（cumulative probability of exclusion, CPE）评估否定父权的可能性。

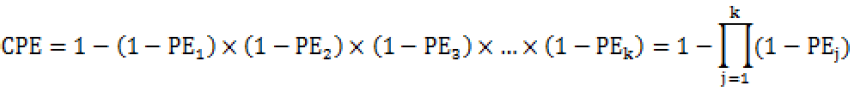
式中：k为遗传标记的数目， 为检测系统中第j个遗传标记的PE值。

3.4.4 多态信息含量 polymorphisminformation content, PIC

遗传标记多态性可提供的信息量的度量，PIC值介于0和1之间，越接近1，则遗传标记的信息量越多。PIC值取决于STR基因座上等位基因数目及频率分布。计算公式如下：

式中：n为等位基因的数目，p_i为基因座上第i个等位基因的频率，p_j为基因座上第j个等位基因的频率。

参 考 文 献

• [1] 侯一平. 法医物证学[M]. 北京:人民卫生出版社, 2016
• [2] 李成涛, 侯一平等. 英汉法医遗传学词典[M]. 北京:科学出版社, 2012.
• [3] Gouy A, Zieger M. STRAF-A convenient online tool for STR data evaluation in forensic genetics[J]. Forensic Sci Int Genet , 2017, (30):148-151.